Quicksort search algorithm

[back]

Quicksort is a sorting algorithm that works by splitting an array into two halves, and during the process of this splitting one element is put in its final position. The resulting "halves" from the split are the elements that need to be to the left and to the right of the finalised element. The splitting process is repeated on each half and each half created by that and so on, until all elements are in their final positions.

This pops out to allow resizing of the window in case you want to try using larger arrays of numbers. Assuming you have Java 1.5 or later, just press the button. If not, download the latest version of Java from www.java.com

What follows is an annotated screenshot of the program. Next is an explanation of the colour code seen in the screenshot, then an explanation of the algorithm and finally source code.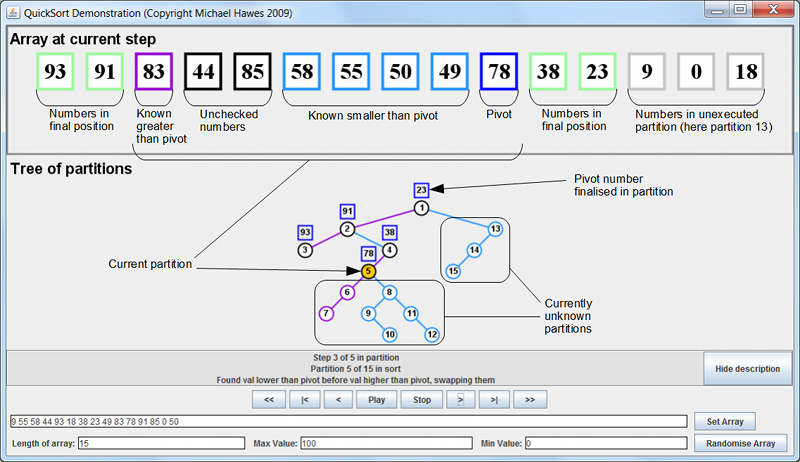

Colour code

We see that numbers in the current partition are shown highlighted in either black, blue, light blue or purple.

Black means we haven't checked that number yet in the current partition execution.

Blue means it is the pivot of the current partition.

Light blue means the algorithm knows it is smaller than the current pivot.

Purple means the algorithm knows it is greater than the current pivot.

Numbers in an inactive partition are shown in grey.

Numbers whose positions have been finalised are shown in green.

Explanation of algorithm

The algorithm centres around the concept of partitions. Each partition in a run of the algorithm achieves the finalisation of the position of one number in the array. The number that will be finalised in execution of a partition is called the pivot of that partition. To begin with we take the entire array as the first partition, in the program displayed as partition 1. To execute a partition we first choose any number in the partition freely as the pivot. You might choose the rightmost number in the partition as the pivot to make it easier to iterate through all the other numbers in the partition, but to demonstrate an alternate pivot choice in the demonstration program we choose a number in the middle of the partition, and swap it with the number at the end of the partition to keep the separation from the other numbers clear.

During the execution of a partition we have to make swaps so that the pivot will have all numbers greater than it on one side, and all numbers lower than it on the other side. If the current partition is a child of another partition (that is, created by executing another partition) there will be numbers that we already know are greater than or less than the current pivot. We can see the boundaries of the current partition, beyond which we already know whether numbers are greater or less than the current pivot, by looking at the tree of partitions. The partition's parents in the tree define its boundaries. To find the boundaries of a single partition in isolation, we can look upwards through the partition tree and the first partition we come to with a pivot less than our current pivot will be one boundary, and the first partition with a pivot greater than our current pivot will be the other boundary. For example, in the screenshot the boundaries of partition 5 are the pivots of partitions 2 and 4. To consider it more seqentially, the boundaries of a partition are the same as the boundaries of its parent partition except with one of the boundaries replaced with the parent's pivot, so that the child partition is bounded by but not including its parent's pivot. Which of the boundaries is replaced by the pivot depends on which side of the partition tree we've gone down, as an execution of a partition results in two new partitions, one for each of the boundaries.

While executing a partition and doing swaps to finalise the position of a partition's pivot, we temporarily ignore the pivot as a part of the current partition. Although in the program we swap the pivot with the last number in the partition, this is not necessary, we merely need to only consider numbers which are in the current partition but are not the pivot. To actually find the final position for the pivot, we keep a left and right cursor which start at the boundaries of the partition and keep moving inward until they find numbers that should not be on that side of the pivot. The purpose of this phase is not only to finalise the position of the pivot but also to put all numbers greater than it on one side of it and all numbers smaller than it on the other side. You move the left cursor right until you find a number that should be on the right side of the pivot, and you move the right cursor left until you find a number that should be on the left side of the pivot. If they meet you've found the position the pivot should be moved to. If they both stop without meeting you've found two numbers that need to be swapped, after which the cursors should continue moving.

Once this swapping stage is complete and the cursors meet, the pivot is moved into position and you can split the remains of the partition into new partitions. The numbers in the current partition apart from the pivot will be split according to which side of the pivot they are on. At this point you know that all numbers are on the side of the pivot that they need to be on in the end. The numbers to the left of the pivot will be one partition, and the numbers to the right will be another. There will be one new partition if there are only numbers on one side of the pivot, and there will be two new partitions if there are numbers on both sides of the pivot. The new partitions can be executed in any order. A partition of only one number does not need to be executed, as you know it is in its final position. When you have no more new partitions to execute, the array is completely sorted.

The Code

You can get the source code here. Just unzip it. Or, you can get the full netbeans project here. Contact me for permission before modifying, copying or using any code in any way other than just running it or looking at it.